今日はクリスマスですね!なので、昨日はクリスマス的な問題を娘に考えてもらいました!ありきたりなケーキの切り分け問題ですが、その背景はちゃんとした算数の基本的な考え方に基づいています。そんな話を少々。
大体の家族なぞなぞはパパが間抜けである
我が家は4人家族です。今日はクリスマスイブ。パパは仕事帰りにショートケーキを買って帰りました。家に着いて箱を開けてみると、そこには上から見ると綺麗な二等辺三角形のショートケーキが3つ入っていました。この3つのショートケーキを4等分する方法を考えてください。

あああ・・・パパ、どんだけ間抜けなんだ・・・。4人家族なのになぜショートケーキを3つ・・・。楽しいクリスマスに争いの種を持ち帰るんじゃないよ・・・。

パパはもう食べてきたから、私たちの分を買ってきたんだよね!
うん、そうであってほしいし、そうでなくても君たちで食べるってことだね。

わたしとおねーちゃんが1つずつ、パパとママは2人で1つだよね!
うん、そうだね、普通は体が大きい大人が多く食べるんじゃないかな??
とりあえず、パパがもう一度、あと1つを買いに行くといいと思いますが、せっかくなので今回の問題を解いてみましょう。
何個だろうが、4等分すれば4人で分けられる
これ、上に乗ったいちごだけなら多分みんな簡単に解けるんですよね。
全てのいちごを縦横に1回ずつ切り、4等分するんです。そうすれば、4等分されたいちごのかけらを3つずつ取れば、4人で3つのいちごを等しく食べられます。つまり、一人3/4個のいちごが食べられるわけです。
これを応用すると、1個のショートケーキから1/4の大きさを切り出すことができれば、何個だろうが4等分できるわけです。
面積の大きさは辺の長さの2乗に比例
二等辺三角形の面積の1/4を作ろうと思うとどうしたらいいか。それを考える上で大切なのが、図形の面積と辺の長さにおける以下の関係です。
相似な図形の面積は、辺の長さの2乗に比例
つまり、面積が1/4になるのは、各辺の長さが1/2の相似な図形を作ることができれば良いということです。そこで、辺の長さを半分にするために、二等辺三角形の辺の中点を結んでみると、二等辺三角形は辺の長さが1/2になった相似な小さい二等辺三角形(つまり面積は1/4)に4分割されます。
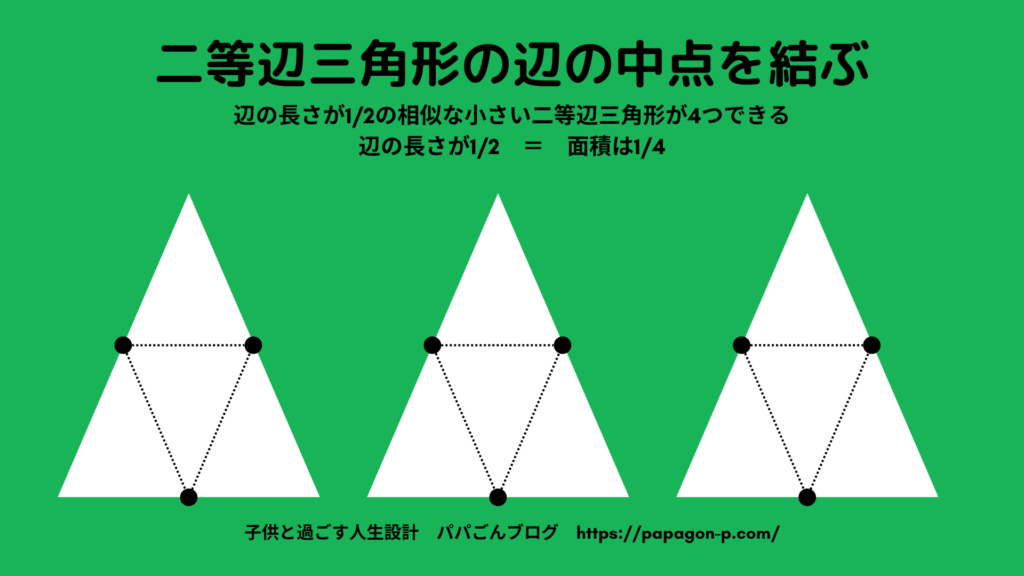
面積が1/4となるのは辺が1/2の相似図形ということに気づくと、問題は簡単になりますね。
より簡単な要素に問題を帰着する
算数では「より簡単な要素に問題を帰着する」ことが問題を解決するための糸口になることが多いです。
今回のような図形の問題に関して言えば、「面積を考えるのであれば、より簡単な辺の長さに問題を帰着する」ことで、さらに言えば、「辺(線分)を半分にするために、より簡単な中点に問題を帰着する」ということを行なっています。
「より簡単な要素に問題を帰着する」図形問題編
体積は 底面積 と 高さ に帰着
面積は 辺(線分) に帰着
線は 点 に帰着
皆さんはどんなクリスマスでしたか?
ということで、本日はクリスマスですね!それにちなんでケーキを切り分ける問題をテーマに考えてみましたが、ちゃんとした算数としての考え方に基づいていることがわかりました。
「ケーキを切れない非行少年たち」という本が昔はやりましたね。しかし今回はそれより酷い、「4人家族なのに3つのケーキを買ってきたパパ」でした。ただ、このパパは、人数どおりにケーキを買って来れない割に、算数の知識・知恵があったから3つのケーキを無事4等分できましたね。世の中、さまざまな知識・知恵が、日常の何気ない問題を解決してくれるものです(4人家族に3つのケーキを買ってくるパパなんて嫌ですが・・・)。
昨晩の我が家は、長女と次女が作ってくれた手作りケーキを四等分して食べました。娘たちの成長を感じながら、とても美味しくいただきました。
それでは、メリークリスマス!






コメント